From EUTERPE to ARGEDION: scaling up the reach of an evolving platform
EUTERPE is being expanded on a larger scale, evolving from its initial concept into a broader platform with increased reach and impact. Learn more at www.argedion.com.
About
“What does the historically unusual behavior of long-term yields imply for the conduct of monetary policy? The answer, it turns out, depends critically on the source of that behavior. To the extent that the decline in forward rates can be traced to a decline in the term premium, ... the effect is financially stimulative and argues for greater monetary policy restraint, all else being equal. ... However, if the behavior of long-term yields reflects current or prospective economic conditions, the implications for policy may be quite different - indeed, quite the opposite”.
Ben Bernanke, Chairman of the Federal Reserve
What is EUTERPE?
The Global Financial Crisis, the eurozone sovereign debt crisis and, more recently, the pandemic shock have all posed considerable challenges to European institutions, monetary authorities and investors. The European Central Bank has been forced to adopt unconventional monetary policy measures, such as negative interest rates and asset purchases, to stabilize financial markets and stimulate economic growth. After more than a decade of near-zero rates, policymakers are currently debating whether the conditions exist to reduce quantitative easing and normalize interest rates. A clear understanding of the forces underlying the movements in interest rates has thus become a timely and very relevant issue for central bankers.
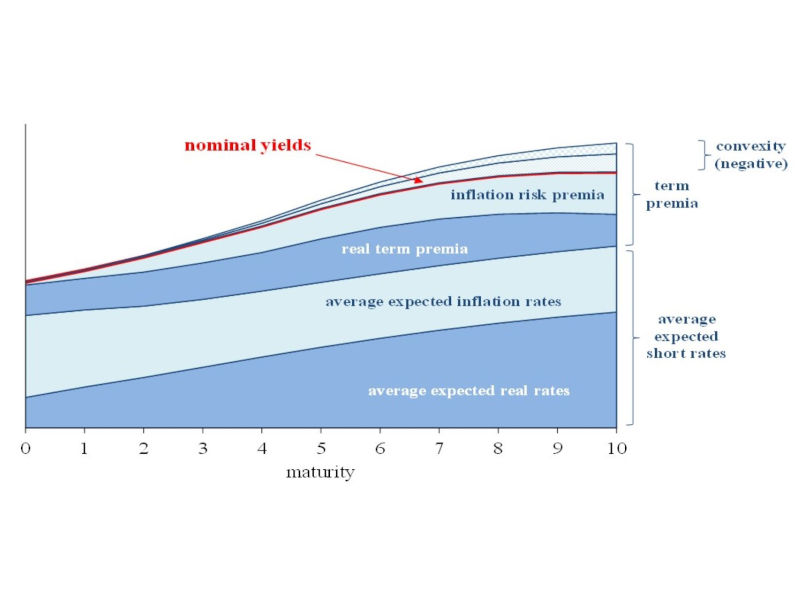
The yield curve is vital for the transmission of monetary policy, as it has a significant influence on asset valuations and is the main driver of the investment and saving decisions of households and firms. From a theoretical viewpoint, nominal yields combine the investors’ expectations on the average short rate over the maturity of the bond with a risk premium component, the term premium, representing the additional compensation they demand to hold a longer-term bond relative to a series of shorter-term bonds and, therefore, reflecting their uncertainty on future interest rates.
The decomposition of yields cannot be inferred directly from market prices and identifying the drivers of yield curve movements in real time is a challenging task. Although extensive theoretical and empirical work has been devoted to this issue, thus far there is neither a commonly accepted framework nor agreement on empirical regularities.

The purpose of the EUTERPE (EUropean TERm Premium Estimation) research project is to provide timely and reliable estimates of the term premium for government bonds of the euro area. EUTERPE not only delivers an academic contribution but also has the ambition to produce a new analytical tool with various applications in the practice of European policymakers and the financial industry.
Funded by the Horizon 2020 initiative of the European Commission, the EUTERPE project is a Marie Sklodowska-Curie Action coordinated by Ca' Foscari University of Venice, under Grant Agreement No 793763.
Methodology
EUTERPE proposes a model for the estimation of term premia in the euro area that relies on an affine term structure framework with interrelations between yields, volatility and macroeconomic factors. The set of the underlying state variables includes both country-specific and global (eurozone-specific) factors, whose dynamics is described by stochastic processes with time-varying volatility.
The term premia of the different countries are interrelated and the strength of those connections depends on the sensitivity of each country to the global factors. From a policymaker perspective, this information is crucial in order to better understand the mechanism of transmission of macro, volatility and global shocks to the risk premium components of bond yields within the euro area.
The model explicitly disentangles the convexity effect from the expectation and risk premium components. This time-varying convexity effect is particularly important for long-term bonds, as it is large and negative at long maturities and is responsible for the persistent downward slope in the term structure of forward rates that is observed in the data.
Using information on euro inflation swaps, we separate the components of nominal forward rates and yields into their inflation and real related elements. In this way, we provide evidence on inflation risk premia and inflation expectations in the eurozone.
The parameters of the state-space representation of the model are estimated by the quasi-maximum likelihood method, with an approximate Kalman filter algorithm being used to calculate the values of the unobserved state variables.
| Technical document | 4.41 M |
Data
Download estimates term premia and average expected short rates
This file contains estimates of the term structure of term premia and average expected short rates for ten countries of the Euro Area and the Euro Area as a whole
| Estimates term premia Last update: 4-Mar-2024 | 837 K |
Download estimates inflation risk premia and expected inflation rates
This file contains estimates of the term structure of inflation risk premia and expected inflation rates for the Euro Area
| Estimates inflation risk premia Last update: 4-Mar-2024 | 64 K |
Term premia and average expected short rates in the Euro Area
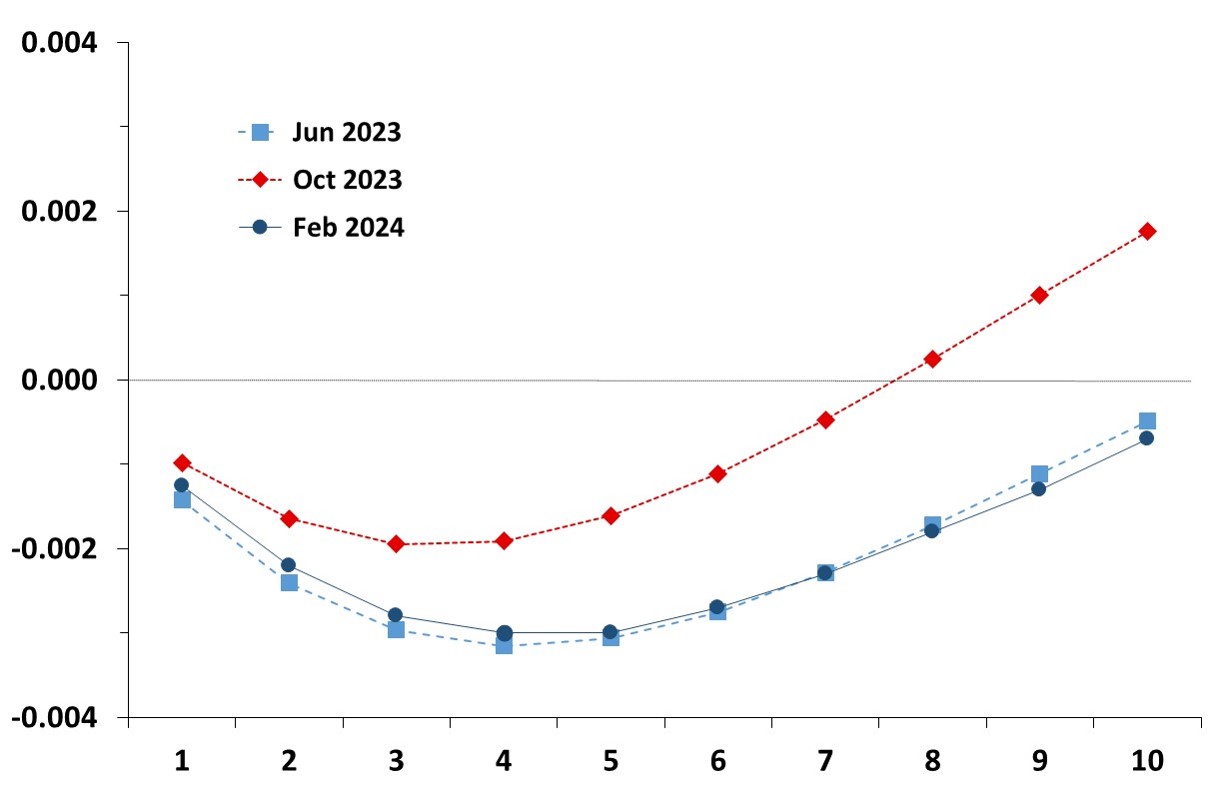
Term structure of term premia in the Euro Area
This graph shows the evolution of the estimated term structure of term premia in the Euro Area
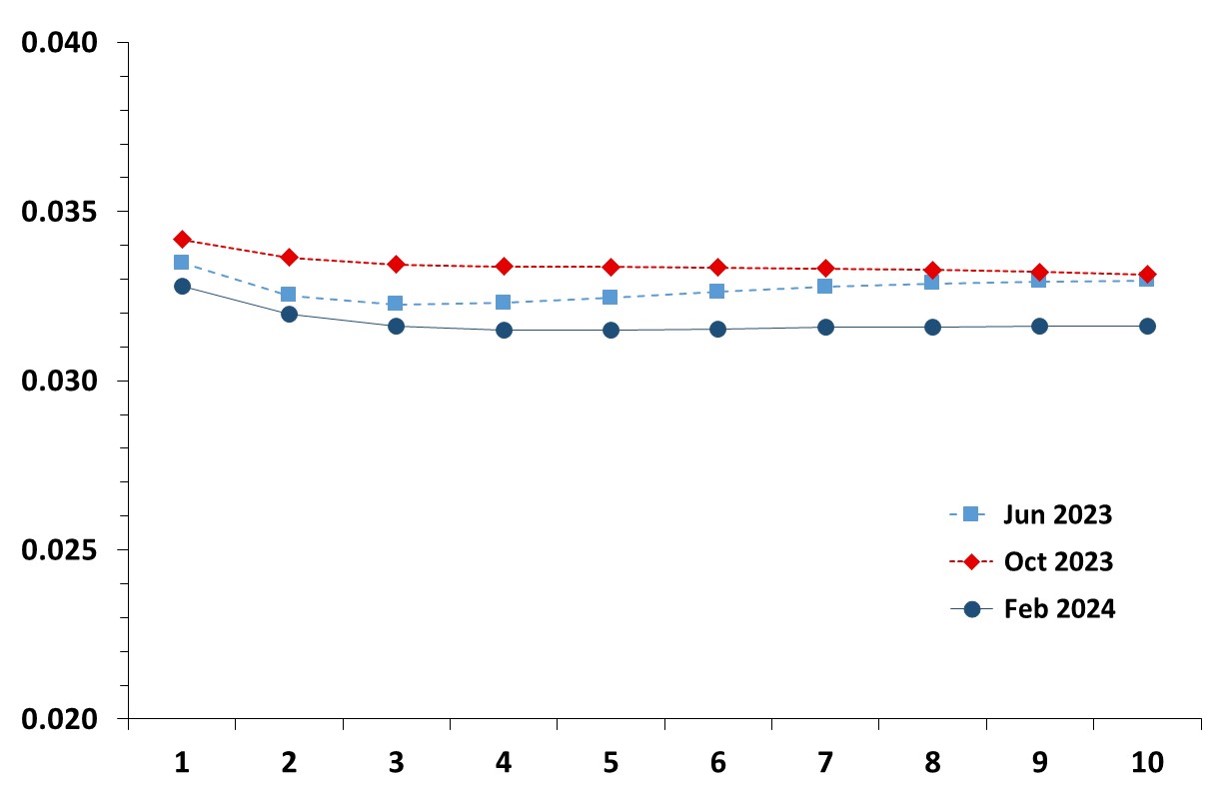
Term structure of average expected short rates in the Euro Area
This graph shows the evolution of the estimated term structure of average expected short rates in the Euro Area
Term premia
Time series estimates of 10-year term premia
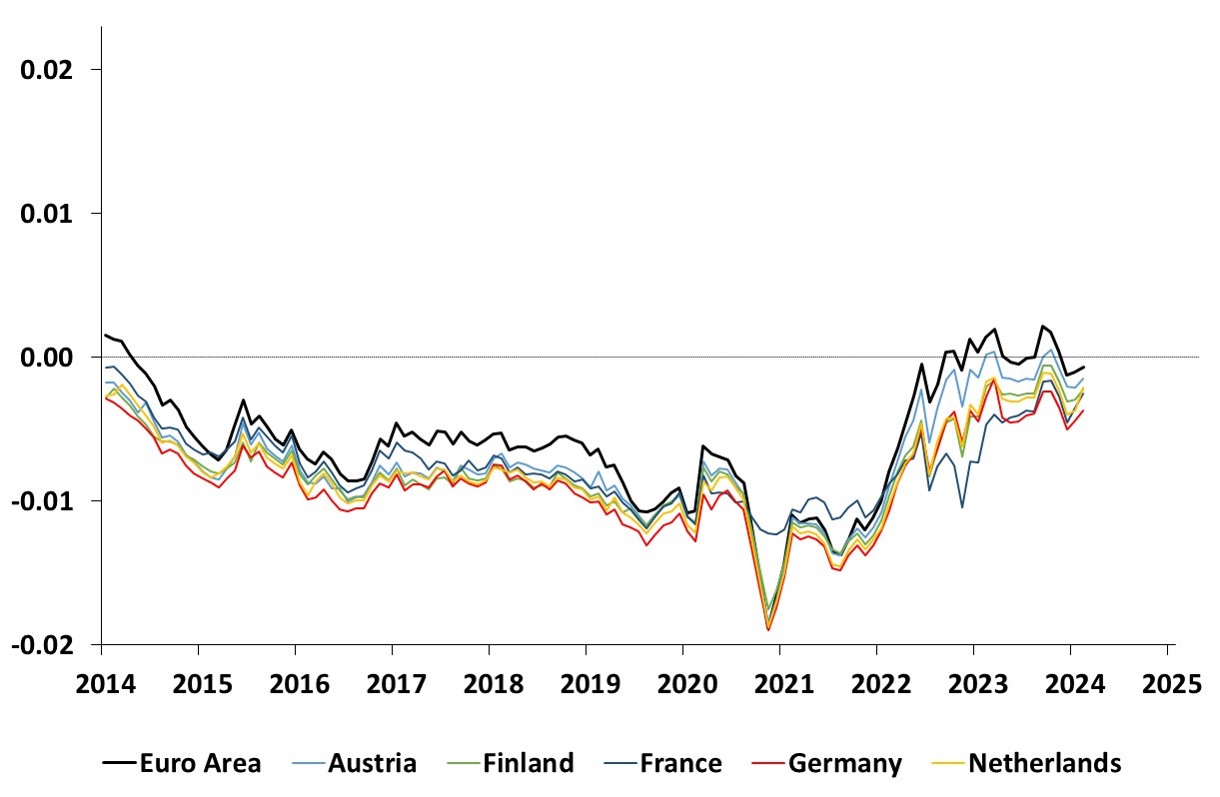
This graph shows the time series estimates of the 10-year term premium for the Euro Area, Austria, Finland, France, Germany and the Netherlands
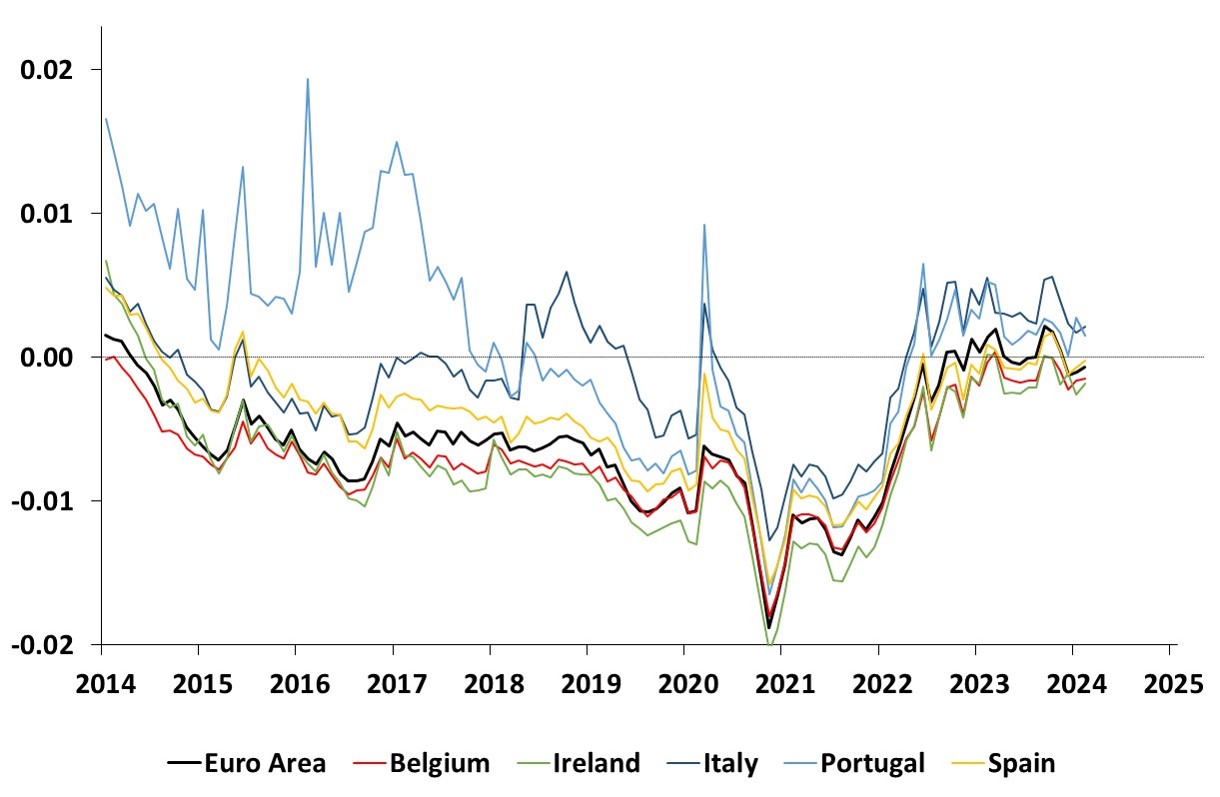
This graph shows the time series estimates of the 10-year term premium for the Euro Area, Belgium, Ireland, Italy, Portugal and Spain
Average expected short rates
Time series estimates of 10-year average expected short rates
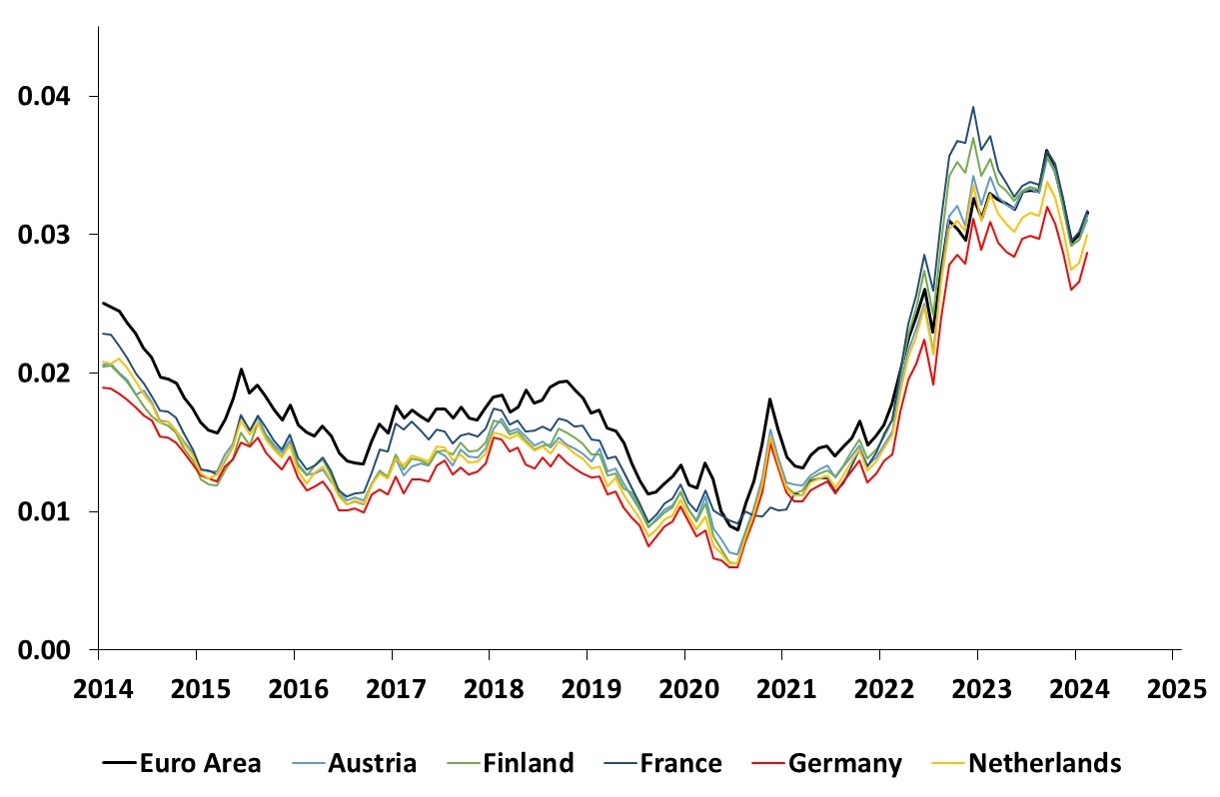
This graph shows the time series estimates of the 10-year average expected short rate for the Euro Area, Austria, Finland, France, Germany and the Netherlands
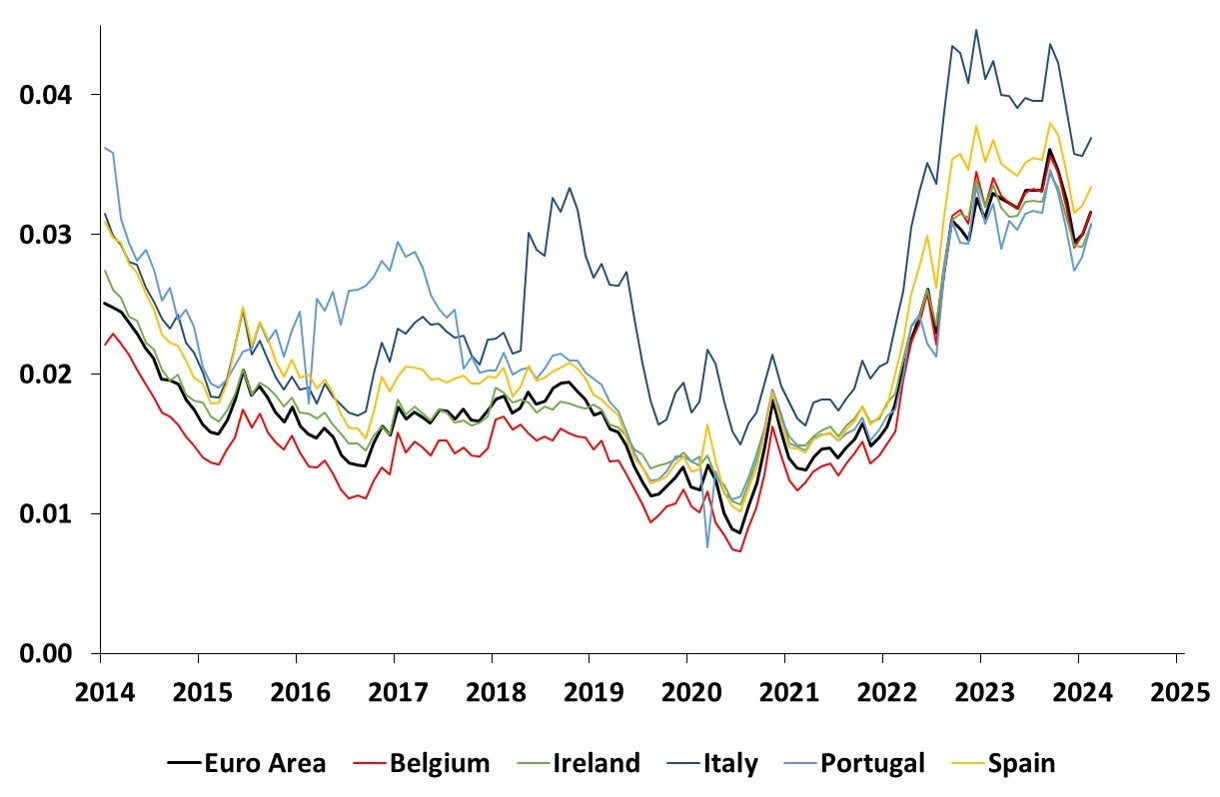
This graph shows the time series estimates of the 10-year average expected short rate for the Euro Area, Belgium, Ireland, Italy, Portugal and Spain
Inflation risk premia and expected inflation rates in the Euro Area
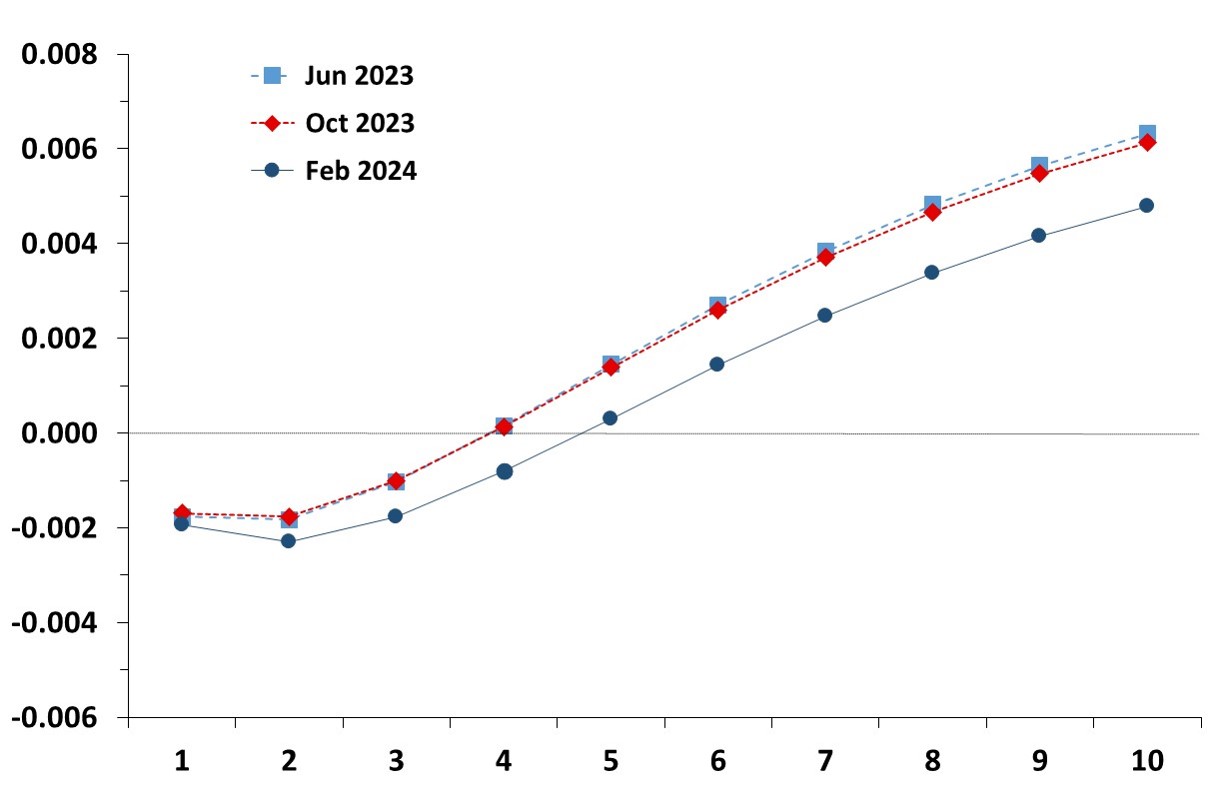
Term structure of inflation risk premia in the Euro Area
This graph shows the evolution of the estimated term structure of inflation risk premia in the Euro Area
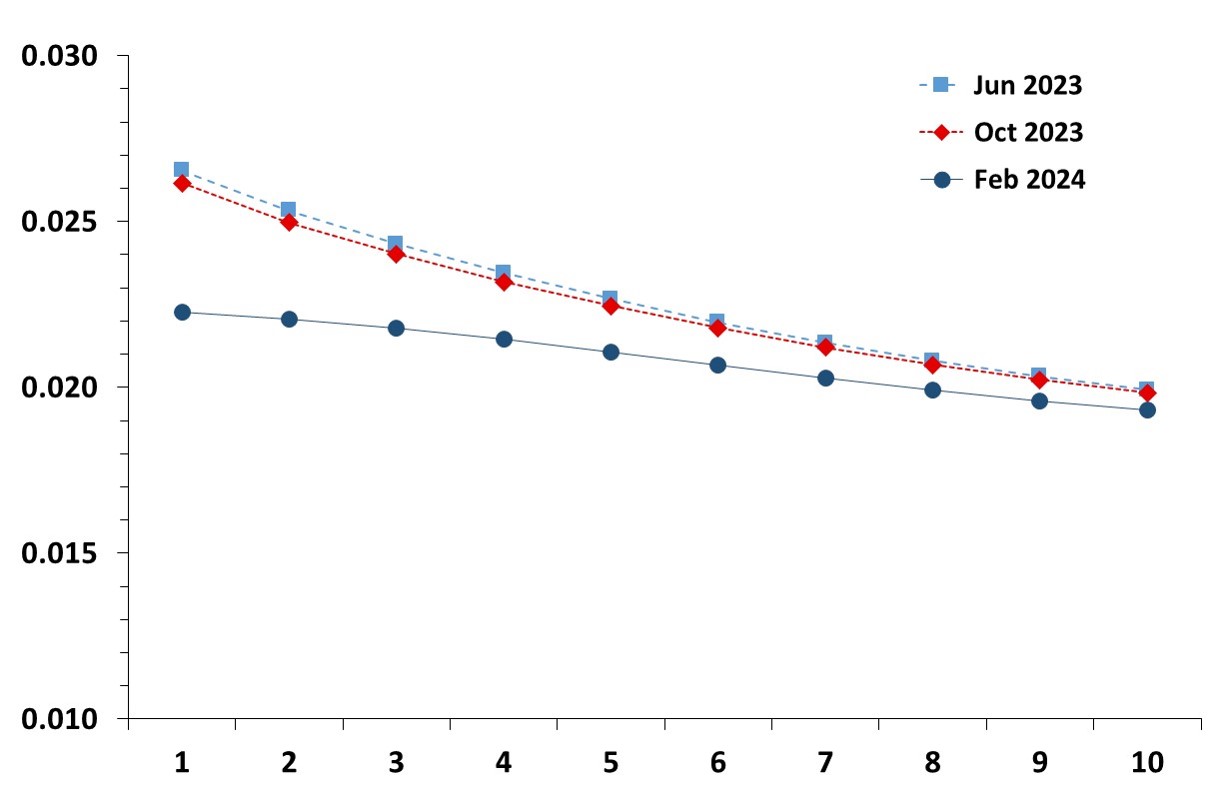
Term structure of expected inflation rates in the Euro Area
This graph shows the evolution of the estimated term structure of expected inflation rates in the Euro Area
Research
Related articles and working papers
Term premia and short-rate expectations in the euro area
Term premia and short rate expectations in the euro area
A. Berardi
Journal of Empirical Finance, 2023, vol.74, 101424
Identifying the components of yields is a challenging task for monetary authorities. We use a term structure model with stochastic volatility and eurozone global macro factors to estimate time-varying term premia and short rate expectations for ten countries in the euro area. Unlike previous studies, we explicitly disentangle from these components the convexity effects that have substantial impact on long-term yields in turbulent times. The empirical evidence shows that term premia are significantly positively related to yield volatility across all countries, while term premia and expected short rates react in opposite directions to shocks in eurozone inflation and GDP growth expectations. A connectedness analysis based on variance decomposition suggests that there exist significant cross-country interconnections for the yield components, with the size of the links varying substantially over time and across countries.
Dissecting the yield curve: the international evidence
Dissecting the yield curve: the international evidence
A. Berardi and A. Plazzi
Journal of Banking and Finance, 2022, vol. 134, 106286
We develop a term structure model that decomposes nominal yields into the sum of an expectation, term premium, and convexity term and in turn of their real and inflation counterparts. The model explicitly captures the interrelation between yield-only and macroeconomic factors while allowing for aggregate stochastic volatility. We extract the components from the nominal and real yield curve of the United States, the Euro Area, the United Kingdom, and Japan. We find that short-rate expectations have steadily declined over the last two decades and account for the bulk of yield dynamics. Term premia increase with maturity but explain a smaller fraction of yield forecast error variance than previously documented. With regard to yield comovement, the United States generates the strongest spillovers at the long end of the yield curve, whereas the Japanese market is the top importer of shocks.
Mind the (convergence) gap: bond predictability strikes back!
Mind the (convergence) gap: bond predictability strikes back!
A. Berardi, M. Markovich, A. Plazzi and A. Tamoni
Management Science, 2021, vol. 67, pp. 7888-7911
We show that the difference between the natural rate of interest and the current level of monetary policy stance, which we label Convergence Gap (CG), contains information that is valuable for bond predictability. Adding CG in forecasting regressions of bond excess returns significantly raises the R2, and restores countercyclical variation in bond risk premia that is otherwise missed by forward rates. Consistent with the argument that CG captures the effect of real imbalances on the path of rates, our factor has predictive ability for real bond excess returns. The importance of the gap remains robust out-of-sample and in countries other than the U.S. Furthermore, its inclusion brings significant economic gains in the context of dynamic conditional asset allocation.
Inflation risk premia, yield volatility, and macro factors
Inflation risk premia, yield volatility, and macro factors
A. Berardi and A. Plazzi
Journal of Financial Econometrics, 2019, vol. 17, pp. 397-431
We incorporate a latent stochastic volatility factor and macroeconomic expectations in an affine model for the term structure of nominal and real rates. We estimate the model over 1999–2016 on U.S. data for nominal and TIPS yields, the realized and implied volatility of T-bonds, and survey forecasts of GDP growth and inflation. We find relatively stable inflation risk premia averaging at 40 basis points at the long end, and which are strongly related to the volatility factor and conditional mean of output growth. We also document real risk premia that turn negative in the post-crisis period, and a non-negligible variance risk premium. We incorporate a latent stochastic volatility factor and macroeconomic expectations in an affine model for the term structure of nominal and real rates. We estimate the model over 1999–2016 on U.S. data for nominal and TIPS yields, the realized and implied volatility of T-bonds, and survey forecasts of GDP growth and inflation. We find relatively stable inflation risk premia averaging at 40 basis points at the long end, and which are strongly related to the volatility factor and conditional mean of output growth. We also document real risk premia that turn negative in the post-crisis period, and a non-negligible variance risk premium.
Saving for retirement in Europe: the long-term risk-return tradeoff
Saving for retirement in Europe: the long-term risk-return tradeoff
A. Berardi and C. Tebaldi
Journal of Pension Economics & Finance, 2023
A comparison of the performances of pension products that ignores long-term trends might significantly overestimate the long-term impact of volatility risks while underestimating the impact of persistent, low frequency trends. This paper proposes a comparison making use of projection models based on the long-term risk-return tradeoff proposed by Campbell and Viceira (2005) to explicitly take into account slow moving economic trends. In order to illustrate the approach and its implications, we discuss the capital protection provided by life-cycle target-date fund strategies and minimum guarantee strategies.
Do long-term yields help to estimate short-term risk premia?
Do long-term yields help to estimate short-term risk premia?
A. Berardi, R. Brown and S. Schaefer
Long-term interest rates are largely ignored in the empirical literature on the term structure and yet contain information that hugely improves the precision of estimates of both risk premia and expectations of future rates. At long maturities the slope of the term structure of risk premia becomes "almost observable" and this provides a strong constraint on the whole term structure of estimated risk premia. Accounting for time variation in yield volatility is key to successful exploitation of the information in long rates. This excludes Gaussian models which perform very poorly in the presence of time-varying volatility.
International evidence on risk premia for nominal and inflation-linked bonds: the information in long-term rates
A. Berardi and S. Schaefer
Using data on yields and their volatility for much longer maturities than usually employed in the literature (up to 25 years), we use a stochastic volatility model to derive estimates of the expectation, risk premium and convexity components of rates for the US, the UK and Germany. Our data includes inflation-linked instruments which allow us to separate the components of nominal yields into their real and inflation-related elements and obtain estimates of the real and inflation risk premium and inflation expectations at any time horizon, including very long-term maturities. The use of long maturity data is motivated by related work that shows that this significantly improves the precision of estimates of risk premia and expectations. At the same time, at long maturities the convexity component is both large and significantly time varying and this requires a model with stochastic volatility.
